Find Cyclic Sum in Java - Programmingempire

The following program determines how to Find Cyclic Sum in Java.

Basically, a cyclic sum is obtained by adding the digits of a number in cyclic order. For instance, if the number = 32188, the cyclic sum = (3+2+1+8+8)+(2+1+8+8)+(1+8+8)+(8+8)+8=22+19+17+16+8=82. Another example, if the number = 9781, cyclic sum=(9+7+8+1)+(7+8+1)+(8+1)+(1)=25+16+9+1=51. Similarly, if the number = 30123, the cyclic sum=(3+0+1+2+3)+(0+1+2+3)+(1+2+3)+(2+3)+(3)=9+6+6+5+3=29. Also, if the number = 6500, the cyclic sum = (6+5+0+0)+(5+0+0)+(0+0)+0=16.

public class CyclicSum
{
	public static void main(String[] args)
	{
		System.out.println("Number = 582109"+" Cyclic Sum = "+findCyclicSum(582109));
		System.out.println("Number = 9781"+" Cyclic Sum = "+findCyclicSum(9781));
		System.out.println("Number = 30123"+" Cyclic Sum = "+findCyclicSum(30123));
		System.out.println("Number = 6500"+" Cyclic Sum = "+findCyclicSum(6500));
	}
	public static int findCyclicSum(int input1)
	{
		int sum=0, n, digits=0, rem, cyclicsum=0, i=0;
		n=input1;
		while(n!=0)
		{
			n=n/10;
			digits++;
		}
		int[] arr=new int[digits];
		n=input1;
		while(n!=0)
		{
			rem=n%10;
			arr[i]=rem;
			i++;
			n=n/10;
		}
		for(i=0;i<=digits-1;i++)
		{
			for(int j=0;j<=digits-1-i;j++)
			{
				sum+=arr[j];
			}
			cyclicsum+=sum;
			sum=0;
		}
		return cyclicsum;
	}
}

Output

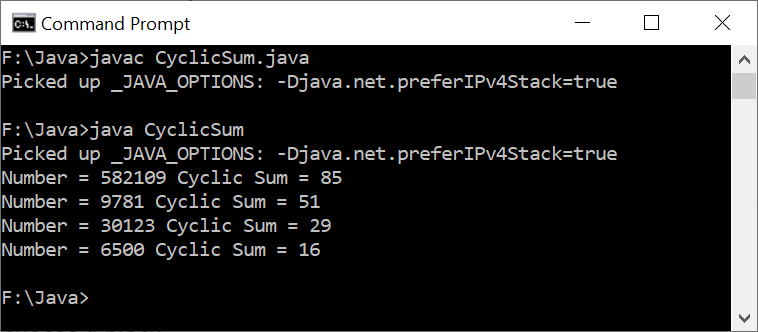
**A Program to Find Cyclic Sum in Java**

Further Reading