C Program to Find the Count of Smaller Neighbour in a Series

The following code shows a C Program to Find the Count of Smaller Neighbour in a Series.

To begin with, let us first define the problem. Suppose we have the following sequence of numbers.

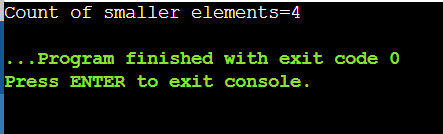
34 6 90 12 5 348 11 113 2 1 55 80

In order to count the smaller neighbour, we must find out whether an element is strictly smaller than both of its neighbours. Therefore, we start with the first element. Also, let us initialise a counter with 0. So, the element 34 >6, so counter remains 0. Likewise, element 6 is less than both 34 and 90, so counter increments by 1. Similarly, 90 is more than 6 and 12, 12 is more than 5. However 5 is smaller than 12 and 348. So counter increments to 2. Similarly, 348 is more than 5 and 11. Whereas, 11 is less than both 348 and 113. So, counter increments to 3. It will not increment for 113, and 2. But, it will increment for 1 and becomes 4. Then, counter will not increment for both 55 and 80. Hence, we get the final output as 4.

Now let us have a look at another test case. The following list shows the elements of the sequence.

3 9 1 89 6 12 19

Since, the first element is smaller than the next one, we get the output as 3. Accordingly, here counter increments for the elements 3, 1, and 6. Similarly, we get an output of 5 for the following list.

12 1 4 9 3 18 6 13 20 5 12 2

The following code shows the complete program.

// Cprogram to count the number of smaller elements

#include <stdio.h>

int main()
{
    int n, i;
    int arr[]={34, 6, 90, 12, 5, 348, 11, 113, 2, 1, 55, 80};
    int elements_count=sizeof(arr)/sizeof(int);
    int counter=0;
    n=elements_count;
    if(arr[0]<arr[1]) counter++;
    if(arr[n-2]>arr[n-1]) counter++;
    for(i=1;i<n-1;i++)
    {
        if((arr[i]<arr[i-1]) && (arr[i]<arr[i+1]))
        {
            counter++;
        }
    }
    printf("Count of smaller elements=%d",counter);

    return 0;
}

Output

Further Reading

50+ C Programming Interview Questions and Answers

C Program to Find Factorial of a Number