How to Implement Merge Sort in C#

This article explains How to Implement Merge Sort in C#.

In fact, Merge Sort is a divide and conquer algorithm that sorts an array by recursively dividing it into two halves, sorting the two halves individually. Then merging the two sorted halves back into one final sorted array. Meanwhile, the merging process involves comparing elements from the two sorted halves and selecting the smaller one to add to the final sorted array. Until it performs merging of all elements from both halves, the process repeats. Evidently, this algorithm has a time complexity of O(n log n), making it a popular choice for sorting large data sets.

Implementation of Merge Sort in C#

The following code calls the MergeSort method recursively, until low becomes greater than high. Whereas, the low represents the minimum value of array index in the respective iteration. Similarly, max represents the maximum value of array index in that iteration. Take the case of the Merge method that performs merging of two halves of the array. Specifically, it takes into consideration, the current elements from both halves of the array and compares them. After that, it places the elements in their correct position.

using System;
namespace MergeSort
{
    class Program
    {
        static void Main(string[] args)
        {
            int[] myarray = {9, 1, 12, -100, 23, 10, -67, -8, -4, 12, 19, 84, 67, 24};
            Console.WriteLine("Array before sorting...");
            foreach (int x in myarray)
                Console.Write(x + "  ");
            Sort.MergeSort(myarray, 0, myarray.Length-1);
            Console.WriteLine("\nArray after sorting...");
            foreach (int x in myarray)
                Console.Write(x + "  ");
            Console.WriteLine();
        }
    }
    class Sort
    {
        public static void MergeSort(int[] myarray, int low, int high)
        {
            if (low < high)
            {
                int mid = (low + high) / 2;
                MergeSort(myarray, low, mid);
                MergeSort(myarray, mid + 1, high);
                Merge(myarray, low, mid, high);
            }
        }
        static void Merge(int[] a, int p, int q, int r)
        {
            int size1 = q - p + 1;
            int size2 = r - q;
            int[] a1 = new int[size1];
            int[] a2 = new int[size2];

            for (int x = 0; x < size1; x++)
            {
                a1[x] = a[p + x];
            }
            for (int x = 0; x < size2; x++)
            {
                a2[x] = a[q+1+x];
            }

            int i = 0;
            int j = 0, k = p;

            while (i < size1 && j < size2)
            {
                if (a1[i] <= a2[j])
                {
                    a[k] = a1[i];
                    i++;
                }
                else
                {
                    a[k] = a2[j];
                    j++;
                }
                k++;
            }

            while (i < size1)
            {
                a[k] = a1[i];
                i++;
                k++;
            }

            
            while (j < size2)
            {
                a[k] = a2[j];
                j++;
                k++;
            }
        }
    }
}

Output

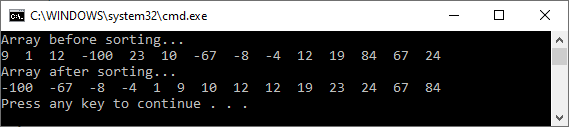
To summarize, we can list the following advantages of Merge Sort.

1. Stable sort. Evidently, Merge sort maintains the relative order of equal elements in the sorted list.
2. Efficient for large data sets. Merge sort has a time complexity of O(n log n), making it suitable for sorting large data sets.
3. Adaptive sorting. In fact, Merge sort performs well even when the input data is partially sorted or reverse sorted.
4. Out-of-place sorting. Merge sort sorts the data in a separate memory space, hence does not modify the original data.
5. Easy to understand. As can be seen, the algorithm is simple to understand and implement.
6. Merge sort can be easily parallelized for distributed computing, making it a popular choice for large scale sorting.

Further Reading

Parameter and ParameterCollection in ADO.NET

Database Manipulation Using DataGrid

Code Render Block in ASP.NET

ASP.NET Practice Exercise

• Angular
• ASP.NET
• C
• C#
• C++
• CSS
• Dot Net Framework
• HTML
• IoT
• Java
• JavaScript
• Kotlin
• PHP
• Power Bi
• Python
• Scratch 3.0
• TypeScript
• VB.NET

Princites